Present Value Calculations
Present Value of a Survival-Adjusted Deferred Perpetuity
This represents the present value of the perpetuity after the death of the relevant individual. The Survival-Adjusted calculations are performed as though the date of death follows the distribution derived from the selected Data Source.
EquationSum for all values of t where each term is:
![D(t) [ v / (d (1+d)^t)]](/assets/eq_perp_SA-f0cf3f6948a1dfefbec7e4b9117d0025349203c71bb0ce9cb637c78be383e499.png)
- D(t) - The probability of an individual's death (or the death of one of a Pair) at t years given their age(s) on the Date of Valuation.
- v - The payment amount.
- d - The discount rate.
- t - All possible number of remaining years.
- n - The maximum number of payments determined by the number of years until age 100 or the set number of maximum payments, whichever is smaller.
Survival-Adjusted Present Value of a Lump Sum on Death
This calculates the Lump Sum based on the probability of death each year. So it is the present value of a lump sum on death of the individual(s). The Survival-Adjusted calculations are performed as though the date of death follows the distribution derived from the selected Data Source.
EquationSum for all values of t where each term is:
![D(t) [v / ((1+d)^t)]](/assets/eq_lump_SA-3dd6fc3c746897ba4b44b460b4e6c402f50e79606d365a6d2ea7e8d91ef6b5bb.png)
- D(t) - The probability of an individual's death (or the death of one of a Pair) at t years given their age(s) on the Date of Valuation.
- v - The payment amount.
- d - The discount rate.
- t - All possible number of remaining years.
- n - The maximum number of payments determined by the number of years until age 100 or the set number of maximum payments, whichever is smaller.
Present Value of a Fixed Date Life Annuity (Certain)
The Fixed Date Life Annuity (Certain) calculates the present value of a Life Annuity assuming the date of death is known. The Mean and Percentiles represent the "known" date of death.
Equation![(v / d) [ 1 - 1 / (1+d)^t ]](/assets/eq_annuity_FD-d5e571cbedf6a4150fa4c6f64fd9aa6ad71240758d16f1434b250cbdfef6596c.png)
- v - The payment amount.
- d - The discount rate.
- t - The number of years projected by the designated percentile.
- g - The assumed rate of constant growth.
- t - All possible number of remaining years.
- n - The maximum number of payments determined by the number of years until age given by the associated percentile in the table or te set number of maximum payments, whichever is smaller.
- k - The number of periods before the first payment.
Present Value of a Fixed Date Annuity (Survival-Adjusted)
The Fixed Date Annuity (Survival-Adjusted) calculates the present value of an Annuity assuming the date of death is either the date given by the Percentile or the set maximum number of payment periods.
EquationSum for all values of t where each term is:
![S(t) [ v * (1+g)^t ] / (1+d)^t](/assets/eq_annuity_SA_a-6e1f0b5ae824dfa560f1ce40ebbd93fcd89b2b579a27bc791f38bb0cf9161f86.png)
The above sum produces the present value as of the deferred number of years. If the deferment period is not zero, then the equation below produces the present value as of the date of valuation.
- S(t) - The probability an individual (or the Pair) will survive t years given their age(s) on the Date of Valuation.
- v - The payment amount.
- d - The discount rate.
- g - The assumed rate of constant growth.
- t - All possible number of remaining years.
- n - The maximum number of payments determined by the number of years until age given by the associated percentile in the table or te set number of maximum payments, whichever is smaller.
- k - The number of periods before the first payment.
Present Value of a Fixed Date Deferred Perpetuity (Certain)
This represents the present value of the perpetuity after the death of the relevant individual. It performs calculation assuming that the individual dies at the given number of years regardless of the probability.
Equation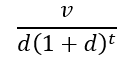
- v - The payment amount.
- d - The discount rate.
- t - The number of years projected by the designated percentile.
Present Value of a Fixed Date (if Alive) Lump Sum (Certain)
This calculates the Lump Sum assuming the date of death is known. It performs calculation assuming that the individual dies at the given number of years regardless of the probability.
Equation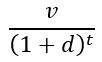
- v - The payment amount.
- d - The discount rate.
- t - The number of years projected by the designated percentile.